Physics 2.5: Electrostatics Flashcards
** coulomb:**
- fundamental unit of charge *
- SI unit of charge*
e= 1.60 x 10-10 C
A proton and an electron each have this amount of charge:
- the proton is positively charged (q = +e),
- the electron is negatively charged (q = − e).
Coulomb’s law
F=(kq1q2)/r2
magnitude of the electrostatic force F between two charges q1 and q2 whose centers are separated by a distance r
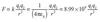
electric field
Electric fields are produced by source charges (q). When a test charge (q0) is placed in an electric field (E), it will experience an electrostatic force (F) equal to q0E.
- If no point charge is present: Efield=kq/r2
- If point change is present: Use this equation to determine the electric field produced by a source charge at a chosen point in space: Efield=F/q0
[Efield is the magnitude of electric field, F is force felt by test charge qo, k is the electrostatic constant, q is the source charge magnitude, and r is the distance between the charges]
stationary charges in an electric field (testing)
stationary test charge: qo the charge placed in the electric field
**stationary source charge: **the charge that sets up the electric field
field lines (lines of force)
- imaginary lines that represent how a positive test charge would move in the presence of the source charge
- drawn in the direction of the actual electric field vectors.
- Field lines also indicate the relative strength of the electric field at a given point in the space of the field
- every charge exerts its own electric field, a collection of charges will exert a net electric field at a point in space that is equal to the vector sum of all the electric fields: Etotal = Eq1 + Eq2 + Eq3 + …
Force in an electric field
force will be generated on the test charge by the electric field:
F=q0E
NOTE: vector equation—be sure to maintain the sign on the charge so that the direction of the force vector is in the direction of qoE.
- +q: the force will be in the same direction as the electric field vector;
- -q: force will be in the direction opposite to the field vector.
Electric Potential Energy
- What is the formula?
- Which gives +U (like charges or unlike charges)?
- Which gives -U?
- related to the relative position of one charge with respect to another charge or to a collection of charges
- one charge q is separated from another charge Q by a distance, r, the charges will have an electric potential energy:
- U=kqQ/r
- Like charges: +U
- Unlike charges: -U
Uelectrical and Work
electrical potential energy for a charge at a point in space in an electric field — the amount of work necessary to bring the charge from infinity to that point.
U=W=Fd
d is the distance r that separates two charges, so
U=W=Fd=Fr = (kqQ/r2)(r)= kqQ/r
Electric Potential
- scalar or vector? (how is the sign determined?)
- Formula with test charge?
- Formula w/o test charge?
- SCALAR: sign is determined by the sign of the charge qo
- the ratio of the magnitude of a charge’s electric potential energy to the magnitude of the charge itself.
- the work necessary to move a charge qo from infinity to a point in an electric field divided by the magnitude of the charge qo
-
With test charge: V=W/qo
*where V is the electric potential measured in volts (V) and 1 volt = 1 joule/coulomb. * -
No test charge: V=kQ/r
*
Voltage: potential difference
- electric potential is inversely proportional to the distance from the source charge, a potential difference will exist between two points that are at different distances from the source charge
- Voltage between a and b is Vb-Va
- Vb-Va = Wob/qo
- Wab is the work needed to move a test charge qo through an electric field from point a to point b.*
- The work depends only on the potentials at the two points a and b and is independent of the actual pathway taken between a and b.*
- Electrostatic force is conservative.*
Electrostatic Work (From V)
Wab is the work needed to move a test charge qo through an electric field from point a to point b.
The work depends only on the potentials at the two points a and b and is independent of the actual pathway taken between a and b.
Charge movement in an Electric Field
- **Positive charge moves spontaneously from high voltage to low voltage. **
- Negative charge moves spontaneously from low voltage to high voltage.
When a positive charge moves spontaneously though an electric field, it will move from a position of higher electric potential (higher electric potential energy divided by the positive charge) to a position of lower electric potential (lower electric potential energy divided by the positive charge).
When a negative charge moves spontaneously through an electric field, it will move from a position of lower electric potential (higher electric potential energy divided by the negative charge) to a position of higher electric potential (lower electric potential energy divided by the negative charge).
Essential Electrostatic Questions
Equipotential Lines
- potential at every point is the same
- potential difference between any two points on an equipotential line is zero
- no work is done when moving a test charge qo from one point to another on an equipotential line.
- Work will be done in moving a test charge qo from one line to another, but the work depends only on the potential difference of the two lines and not on the pathway taken between them.
Electric Dipole
- Dipole moment is a VECTOR
- results from two equal and opposite charges being separated a small distance d from each other
- can be transient or permanent
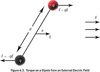
net torque experienced by an electric dipole about the center of the dipole axis due to an external electric field
τ=pEsinø
where p is the magnitude of the dipole moment (p = qd), E is the magnitude of the uniform external electric field, and theta is the angle the dipole moment makes with the electric field. This torque will cause the dipole to reorient itself by rotating so that its dipole moment, p, aligns with the electric fieldE.
