Physics 4: Light & Sound

Question 1

Monochromatic light of a certain wavelength falls on a narrow slit. On a screen a certain distance away, the distance between the second minimum and the central maximum is 2cm. What would happen to the spacing between the two if the wavelength of the radiation were increased?

• a) It would depend on whether the new wavelength is an odd or even multiple of the old.
• b) It would remain unchanged
• c) It would decrease.
• d) it would increase.

Answer 1

D. It would increase.

Question 2

Electromagnetic Spectrum

Answer 2

The following units are often used when quoting wavelengths:

• 1 mm = 10^{− 3}m,
• 1 μ m = 10^{− 6} m,
• 1 nm = 10^{− 9} m, and
• 1 Å (angstrom) = 10^{− 10} m.

The full spectrum is broken up into many regions, which in descending order of wavelength are

• radio (10⁹ m− 1 m),
• microwave (1 m− 1 mm),
• infrared (1 mm− 700 nm),
• visible light (700 nm− 400 nm),
• ultraviolet (400 nm− 50 nm),
• x-ray (50 nm− 10− 2 nm), and
• gamma rays (less than 10− 2 nm).

Question 3

electromagnetic waves

Question 4

speed of light

Answer 4

c=3 × 10⁸m/s

c=fλ

Question 5

blackbody

Answer 5

• used to describe an ideal radiator
• refers to the fact that such an object is also an ideal absorber and would appear totally black if it were at a lower temperature than its surroundings

Question 6

rectilinear propagation

Answer 6

When light travels through a single homogeneous medium, it travels in a straight line

Question 7

geometrical optics.

Answer 7

behavior of light at the boundary of a medium or interface between two media is described by this theory

Question 8

law of reflection

Answer 8

θ ₁=θ_{<span>2</span>}

where θ ₁ is the incident angle and θ ₂ is the reflected angle, both measured from the normal

Question 9

real image

Answer 9

light actually converges at the position of the image

Question 10

virtual image

Answer 10

light only appears to be coming from the position of the image but does not actually converge there.

• Because the light does not converge at all, plane mirrors always create virtual images

Question 11

center of curvature (C)

Answer 11

a point on the optical axis located at a distance equal to the radius of curvature from the vertex of the mirror;

in other words, where the center of the mirrored sphere would be, were it a complete sphere.

Question 12

radius of curvature (r)

Answer 12

a measure of the radius of the circular arc which best approximates the curve at that point

Question 13

Focal length (for all spherical mirrors)

Answer 13

f=r/2

Question 14

Key Variable Distances for Geometrical Optics

Answer 14

The focal length (f) is the distance between the focal point (F) and the mirror (for all spherical mirrors,

, where the radius of curvature (r) is the distance between C and the mirror); the distance of the object from the mirror is o; the distance of the image from the mirror is i

Question 15

Mirror Equation

Answer 15

(1/o) + (1/i) = 1/f =1/f = 2/r

• _Plane mirrors_ can be thought of as infinitely large spherical mirrors.
• As such, for a plane mirror, r = f = ∞ , and the equation becomes: (1/o) + (1/i) = 0
• or : i= (-o)

Question 16

magnification (m)

Answer 16

** dimensionless value that is the ratio of the image’s height to the object’s height**

m= -(i/o)

• A negative magnification signifies an inverted image, while
• a positive value means the image is upright.
• If |m| < 1, (“absolute value of m is less than 1”) the image is reduced; i
• f |m| > 1, the image is enlarged; and
• if |m| = 1, the image is the same size as the object.

Question 17

Ray Diagrams for Concave Spherical Mirror at 3 Different Points

Answer 17

• In Figure 10.6a, the object is placed between F and C, and the image produced is real, inverted and magnified.
• In Figure 10.6b, the object is placed at F, and no image is formed because the reflected light rays are parallel to each other. In terms of the mirror equation, we say that the image distance i = ∞ here.
• Figure 10.6c, the object is placed between Fand the mirror, and the image produced is virtual, upright, and magnified.

Question 18

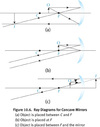
In general, there are three important rays to draw..

What are they?

Answer 18

1. For a concave mirror, a ray that strikes the mirror parallel to the horizontal is reflected back through the focal point.
2. A ray that passes through the focal point before reaching the mirror is reflected back parallel to the horizontal.
3. A ray that strikes the mirror right where the normal intersects it gets reflected back with the same angle (measured from the normal).

Question 19

Sign Chart for Single MIrrors

Answer 19

Symbol

Positive (+)

Negative (-)

o

Object is in front of the mirror (R-side)

Object is behind mirror (V-side)

i

Image is in front of mirror (R-side)

Image is behind mirror (V-side)

r

Concave mirrors

Convex mirrors

f

Concave mirrors

Convex mirrors

m

Image is upright (erect)

Image is inverted

Question 20

Snell’s Law of Refraction

Answer 20

n₁sin θ₁= n₂sin θ₂

Question 21

index of refraction of the medium.

Answer 21

n=c/v

• For air, n is essentially equal to 1 because v≈ c.
• But for all other materials on MCAT: ** v < c and n > 1.**

Question 22

General Bending concepts moving between indecies of different n-values:

Answer 22

• when light enters a medium with a higher index of refraction (n2 > n1), it bends towards the normal so that θ 2 < θ 1
• if the light travels into a medium where the index of refraction is smaller (n2 < n1), the light will bend away from the normal so that θ 2 > θ 1.

Question 23

Total internal reflection

Answer 23

all the light incident on a boundary is reflected back into the original material, results for any angle of incidence greater than the critical angle, θ c

sinθ _c=n₁/n₂

Question 24

THIN SPHERICAL LENSES

Answer 24

two surfaces that affect the light path

Because light can be coming from either side of a lens, a lens has two focal points (one on each side of the lens) and the focal length can be measured in either direction from its center

Question 25

basic formulas for finding image distance and magnification

Answer 25

(apply as those from spherical mirrors)

Question 26

lensmaker’s equation

Answer 26

For lenses where the thickness cannot be neglected, the focal length is related to the curvature of the lens surfaces and the index of refraction of the lens by:

1/f =(n-1) [(1/r₁₎-(1/r₂)]

where n is the index of refraction of the lens material, r1 is the radius of curvature of the first lens surface and r2 is the radius of curvature of the second lens surface.

Question 27

Sign Chart for Single Lenses

Answer 27

Symbol

Positive

Negative

o

Object on side of lens light is coming from (V side)

Object on side of lens is going to (R side)

i

Image on side of lens light is going to (R side)

Image on side of lens light is coming from (V side)

f

Converging lens

Diverging lens

m

Image erect

Image inverted

r

When on R side (convex surface as seen from side the light is coming from)

When on V side (concave surface as seen from side light is coming from)

Question 28

power (P).

Answer 28

diopters, where f (the focal length) is in meters and is given by this equation:

P=1/f

P has the same sign as f and is, therefore, positive for a converging lens and negative for a diverging lens.

Question 29

Lenses in contact

Answer 29

series of lenses with negligible distances between them. These systems behave as a single lens with equivalent focal length given by

Question 30

lenses not in contact,

Answer 30

image of one lens is used to make the object of another lens

Question 31

dispersion

Answer 31

n=c/v

Question 32

Diffraction

Answer 32

As the slit is narrowed, the light spreads out more. This spreading out of light as it passes through a narrow opening=diffraction

Dark fringes:

**a sin θ = nλ **

where a is the width of the slit, λ is the wavelength of the incident wave, and θ is the angle made by the line drawn from the center of the lens to the dark fringe and the line perpendicular to the screen.

Question 33

Image of Diffraced Wave

Question 34

Image of Diffraction Grating and Light Scattering

Question 35

Interference

Question 36

Plane-polarized light

Answer 36

ight in which the electric fields of all the waves are oriented in the same direction

Question 37

Unpolarized light

Answer 37

random orientation of its electric field vectors; sunlight and light emitted from a light bulb are prime examples

Question 38

Essential Equations for Optics

Question 39

Photoelectric Effect

Question 40

work function of the metal

Answer 40

We can calculate the maximum kinetic energy of the ejected electron with the formula:

K_max = hf - W

The work function is the minimum energy required to eject an electron and is related to the threshold frequency of that metal by

W=hf_T

_{If the frequency of the incident photon is less than the threshold frequency (f<fT), then no electron will be ejected because the photon doesn’t have sufficient energy to dislodge the electron from its atom. But if the frequency of the incident photon is greater than the threshold frequency (f>fT), then an electron will be ejected, and the maximum kinetic energy of the ejected electron will be equal to the difference betweenh fandhfT.}

Question 41

Energy Levels of Hydrogen

Question 42

change in energy of an electron due to absorption or emission of a photon.

Answer 42

equation to determine the change in energy of an electron due to absorption or emission of a photon

delta E = E_f-E_i

determine the change in energy of an electron due to absorption or emission of a photon.

hf= absolute value of delta E

The absolute value sign around Δ E represents the fact that negative frequencies do not exist, so the apparent sign of Δ Eis irrelevant once you know

Question 43

Bohr Postulates

Answer 43

1. Energy levels of the electron are stable and discrete. They correspond to specific orbits.
2. An electron emits or absorbs radiation only when making a transition from one energy level to another (from one allowed orbit to another).
3. To jump from a lower energy (inner orbit) to a higher energy (outer orbit), an electron must absorb a photon of precisely the right frequency such that the photon’s energy (hf) equals the energy difference between the two orbits.
4. When jumping from a higher energy (outer orbit) to a lower energy (inner orbit), an electron emits a photon of a frequency such that the photon’s energy (hf) is exactly the energy difference between the two orbits.

Question 44

Essential Equations of Atomic Phenomena

Question 45

Exponential Decay

Answer 45

rate:

(where λ is known as the decay constant.)

Exponential decay:

Relation to half life: