Physics I: 6-8 Flashcards
fluids
substances that have the ability to flow and conform to the shapes of their containers
fluids can exert ____ forces, but cannot exert ____ forces
perpendicular
shear
shear forces
tangential forces
density
ρ
mass per unit volume of a substance (fluid or solid)
scalar
density eq
ρ = m/V
density of water
1 g/cm3 = 1000 kg/m3
weight in terms of density eq
Fg = ρVg
V = volume
specific gravity eq
ρ / 1 g/cm3
pressure
P
ratio of the force per unit area
scalar
pressure in terms of force eq
P = F/A
F = magnitude of normal force
SI unit
pressure
pascal Pa
why is pressure scalar rather than vector?
pressure is the same at all points along the walls of its container and within the space of the container itself
pressure applies in all directions at any point
atmospheric pressure
changes with altitude
pressure exerted by a gas against the walls of its container will always be ________ to the container walls
perpendicular (normal)
absolute (hydrostatic) pressure
total pressure exerted on an object that is submerged in a fluid
sum of all pressures at a certain point within a fluid
absolute pressure eq
P = P0 + ρgz
P0 = incident or ambient pressure
z = depth of object
gauge pressure
difference between absolute pressure and atmospheric pressure
amount of pressure in a closed space above and beyond atmospheric pressure
gauge pressure eq
Pgauge = P - Patm = (P0 + ρgz) - Patm
when does the gauge pressure equal the fluid pressure?
when atmospheric pressure is the only pressure above the fluid column
hydrostatics
study of fluids at rest and the forces and pressures associated with standing fluids
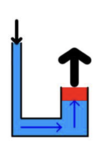
pascal’s principle
a pressure applied to an incompressible fluid will be distributed undiminished throughout the entire volume of the liquid
hydraulic machines
operate based on the application of pascal’s principle to generate mechanical advantage
generate output force by magnifying an input force by a factor equal to the ratio of the cross sectional area of the larger piton to that of the smaller piston
hydraulic lift eqs
according to pascal’s principle, the larger the area, the ___ the force…
larger
although this force will be exerted through a smaller distance
archimedes principle
buoyant force
a body wholly or partially immersed in a fluid will be buoyed upwards by a force equal to the weight of the fluid that it displaces
the direction of the buoyant force is always __ to the direction of gravity
opposite
if the max buoyant force is larger than the force of gravity on the object, the object will ___
float
this will be true if the object is less dense than the fluid it is in
if the max buoyant force is smaller than the force of gravity on the object, the object will ___
sink
this will be true if the object is more dense than the fluid it is in
how would the buoyancy differ between two objects placed in a fluid if they displace the same volume of fluid?
they will experience the same magnitude of buoyant force even if the objects themselves have different masses
how to calculate the percent of an objects volume that is submerged?
express the object’s specific gravity as a percent - indicates the percent of the object’s volume that is submerged (when the fluid is pure water)
surface tension
causes liquid to form a thin but strong layer at the liquids surface
results from cohesion
cohesion
the attractive force that a molecule of liquid feels toward other molecules of the same liquid
adhesion
attractive force that a molecule of liquid feels toward the molecules of some other substance
meniscus
curved surface in which liqudi crawls up the side of the contain
forms when adhesive forces are greater than cohesive forces
backwards (convex) meniscus
forces when cohesive forces are greater than adhesive forces
what will form when adhesive forces are greater than cohesive forces?
meniscus
what will form when cohesive forces are greater than adhesive forces?
backwards meniscus
what would the meniscus of a liquid that experiences equal cohesive and adhesive forces look like?
no meniscus
surface would be flat
a block is fully submerged 3 in below the surface of a fluid, but is not experiencing any acceleration. what can be said about the displaced volume of fluid and the buoyant force?
The displaced volume is equal to the volume of the block. The buoyant force is equal to the weight of the block, and is equal to the weight of the displaced fluid. By extension, the block and the fluid in which it is immersed must have the same density.
T/F
to determine the volume of an object by fluid displacement it must have a specific gravity greater than 1
F
a fluid with a low specific gravity can be used instead of water to determine volumes of objects that would otherwise float in water
to which side of a hydraulic life would the operator usually apply a force - the side with the larger cross sectional area, or the side with the smaller cross sectional area? why?
smaller
because pressure is the same on both sides of the life, a smaller force can be applied on the smaller surface area to generate the desired pressure
fluid dynamics
study of fluids in motion
viscosity
η
resistance of a fluid to flow
viscous drag
nonconservative force generated by viscosity
examples of thin fluids
gases, water, dilute aqueous solutions
thin fluids have __high/low__ viscocity, making them flow __faster/slower__
low
faster
low viscous drag
thick fluids have __high/low__ viscocity, making them flow __faster/slower__
high
slower
more viscous fluids will __lose/gain__ energy while flowing
lose
laminar flow
smooth and orderly
layers of fluid that flow parallel to each other (layers do not necessarily have the same linear speed)
the layer closest to the wall of a pipe flowers __slower/quicker__ than the more interior layers of fluid
slower
poiseuille’s law
determines rate of laminar flow
poiseuille’s law
relationships
radius and pressure gradient - inverse exponential to fourth power
slight change in radius of the tube has a significant effect on the pressure gradient, assuming a constant flow rate
turbulent flow
rough and dissorderly
causes the formation of eddies
eddies
swirls of fluid of varying sizes ocurring typically on the downstream side of an obstacle
critical speed
depends on physical properties of the fluid
such as viscosity and diameter of tube
boundary layer
thin layer of fluid adjacent to the wall
turbulence can arise when speed of fluid exceeds the …
critical speed
what happens when critical speed for a fluid is exceeded?
- fluid demonstrates complex flow patterns
- laminar flow occurs only in boundary layer
- flow speed is zero and increases uniformly throughout thee layer
- beyond the boundary layer, motion is highly irregular and turbulent
reynolds number
NR
constant that depends on the physical characteristics of the objects within the fluid
critical speed eq
vc = critical speed
NR = reynolds number
streamlines
indicate the pathways followed by tiny fluid elements as they move
never cross each other
linear speed
measure of the linear displacement of fluid particles in a given amount of time
continuity equation tells us
fluids will flow more quickly through narrow passages and more slowly through wider ones
conservation of mass
linear speed of a fluid ___inc/dec___ with decrease cross sectional area
increases
flow rate and cross sectional area relationship
flow rate is constant in a tube regardless of cross sectional area
flow rate eq
Q = v1A1 = v2A2
Q = flow rate
v = linear speed
A = cross sectional area
on MCAT, incompressible fluids are assumed to have…
laminar flow and very low viscosity while flowing, allowing us to assume conservation of energy
Bernoulli’s eq
h = height of fluid above some datum
dynamic pressure
pressure associated with the movement of a fluid
essentially the KE
dynamic pressure eq
1/2 ρv2
static pressure eq
P + ρgh
bernoulli’s eq states
the sum of the static pressure and dynamic pressure will be constant within a closed container for an incompressible fluid not experiencing viscous drag
energy conservation: more energy dedicated toward fluid movement means less energy dedicated toward static fluid pressure
more energy dedicated toward fluid movement means _more/less_ energy dedicated toward static fluid pressure
less
pitot tubes
specialized measurement devices tha tdetermine the speed of a fluid flow by determining the difference between the static and dynamic pressure of the fluid at given points along a tube
venturi flow meter
venturi effect
for a horizontal flow, there is an inverse relationship between pressure and speed
in a closed system, there is a direct relationship between cross sectional area and pressure exerted on the walls of the tube
how do the following concepts relate to one another: venturi effect, bernoulli’s eq, continuity eq? what relationship does each describe?
The continuity equation describes the relationship of flow and cross-sectional area in a tube, while Bernoulli’s equation describes the relationship between height, pressure, and flow. The Venturi effect is the direct relationship between cross-sectional area and pressure, and results from the combined relationships of the Bernoulli and continuity equations.
what effect woudl increasing each of the following have on flow rate: radius of the tibe, pressure gradient, viscosity, length of the tube?
flow rate inc when inc radius or pressure gradient
dec when inc viscosity or length
Which of the following are the defining characteristics of all fluids?
I. Flow when forces are exerted on them.
II. Can take the shape of their container.
III. Be less dense than their solid counterparts.
(A) I only
(B) I and II only
(C) II and III only
(D) I, II and III
(B) I and II only
Two defining characteristics of fluids are that they flow and conform to their container’s shape.
Note that most fluids are less dense than their solid counterparts, but there are exceptions like water!
What is the key difference then between a gas and a liquid?
Liquids are incompressible, while gases are compressible.
What is Pascal’s principle (relationship between pressure in and pressure out)? How do the forces in and out relate to this concept?
Pressure in = Pressure out
Because of this, the forces are related to the area: F1/A1 = F2/A2 = Pressure in = Pressure out
Imagine I have a half-full, closed bottle of soda. According to Pascal’s Principle, if I try to squeeze this bottle, to which of the following places would the change in pressure be transmitted?
I. The liquid soda
II. The air above the soda
III. The soda bottle
(A) I only
(B) I and II only
(C) I and III only
(D) I, II and III
(D) I, II and III
If I tried to squeeze a half-full, closed bottle of soda, then each of the following would have the change in pressure affect it equally:
I. The liquid soda
II. The air above the soda
III. The soda bottle
Incompressible fluids in closed container will distribute the increased pressure to all of the fluid and the container’s walls!
A liquid is in a horseshoe shaped test tube with one side large than the other. If a force of 9.67 N is spread across the liquid with an area of 1.89 m^2, what would the force of the liquid be on the other side of the test tube, which has an area of 13.24 m^2?
(A) 45.63
(B) 67.74
(C) 89.40
(D) 112.89
B) 67.74
F1/A1 = F2/A2 (9.67)/(1.89) = F2/(13.24) F2 = approx. 70 N (actual: 67.74)
What is the equation for pressure of a fluid at a given depth in terms of density (with no atmosphere)?
Pressure = ρhg
ρ = density h = depth from top of fluid g = acceleration due to gravity (9.8 m/s^2)
What is the pressure of water in a vacuum at a depth of 4.78 m?
(A) 46,844 Pa
(B) 57,391 Pa
(C) 89,648 Pa
(D) 104,589 Pa
(A) 46,844 Pa
ρH2O = 1000 kg/m^3
Pressure = ρhg Pressure = (1000)(4.78)(9.8) Pressure = 49,000 pascals (actual: 46,844)
What is the equation for buoyancy force?
Buoyancy Force = Weight of liquid displaced (in N) = Vρg
True or false? My buoyant force in a fluid with a low specific gravity ( <1)will be greater than my buoyant force in water.
False. My buoyant force in a fluid with a low specific gravity ( <1)will be LESS than my buoyant force in water.
This is because that buoyant force is dependent upon the weight of the fluid displaced, so a more dense (higher specific gravity) fluid will have a stronger buoyant force!
An object with a weight of 97.89 N is submerged in water, and has a net force of 46.57 N acting on it. What is the volume of the object?
(A) 5.67⋅10^3
(B) 9.88⋅10^1
(C) 2.43⋅10^-1
(D) 4.75⋅10^-3
(D) 4.75⋅10^-3
Weight of object = 100 N
Net force = 50 N
Buoyant force = 50 N
ρ of water= 1000kg/ m^3
Buoyant force = Vρg
46.57 = V (1000)(9.8)
V = 4.9⋅10^-3 m^3 (actual: 4.75⋅10^-3 m^3)
What is the equation of continuity? What is the purpose of this equation?
v1A1 = v2A2
v1 = velocity in
A1 = area in
v2 = velocity out
A2 = Area out
Compares flow of fluid in a pipe of varying cross sectional area.
Absolute (Hydrostatic) Pressure combines both the ambient pressure and the pressure the fluid exerts. Write the equation for Absolute Pressure out.
P = Po + ρgh
P = Absolute Pressure (Pa or N/m^2) Po = Pressure at Surface (usually equivalent to atmospheric pressure) (Pa) ρ = Density (kg/m^3) g = Acceleration due to Gravity (9.8 m/s^2) h = Height (m)
Compare Absolute Pressure and Gauge Pressure.
Absolute Pressure includes both the Ambient Pressure and the pressure a fluid is exerting.
Gauge Pressure is the difference between Absolute Pressure and the Atmospheric pressure.
The most simple of the flow rate equations relies upon the cross-sectional area of the pipe and one other factor. Write out this fundamental Flow Rate equation.
f = Av
f = flow rate A = Cross-sectional area v = velocity of the fluid
What is Bernoulli’s equation in terms of pressure, height, and velocity of a fluid at two points in a pipe?
P1 + 1/2ρv1^2 + ρgh1 = P2 + 1/2ρv2^2 + ρgh2
P1 = Pressure at Point 1 (Pa) P2 = Pressure at Point 2 (Pa) ρ = Density of the Fluid (kg/m^3) v1 = Velocity at Point 1 (m/s) v2 = Velocity at Point 2 (m/s) g = Acceleration due to Gravity (9.8m/s^2) h1 = Height at Point 1 (m) h2 = Height at Point 2 (m)
Another way to look at this is as Wi + PEi + KEi = Wo + PEo + KEo, where i is for input and o is for output
Fill in the blanks: In Bernoulli’s Equation, the terms can be grouped into two different types of pressures. P + ρgh can be referred to as ___________ and 1/2ρv^2 can be referred to as ____________.
(A) Static Pressure, Dynamic Pressure
(B) Dynamic pressure, Static Pressure
(C) Dynamic Pressure, Environmental Pressure
(D) Environmental Pressure, Dynamic pressure
(A) Static Pressure, Dynamic Pressure
In Bernoulli’s Equation, the terms can be grouped into two different types of pressures. P + ρgh can be referred to as Static Pressure and 1/2ρv^2 can be referred to as Dynamic Pressure.
Water is flowing through a pipe of varying cross sectional area down a hill with a velocity of 10 m/s at the top and 20 m/s at the bottom. Over this distance, the pipe goes from a height of 10 m to a height of 0 m. The water is at a pressure of 1,000,000 Pascals at the top. What is the pressure at the bottom (use 10 m/s^2 for g for simplicity)?
(A) 820,000
(B) 950,000
(C) 1,240,000
(D) 1,560,000
(B) 950,000
P1 + 1/2ρv1^2 + ρgh1 = P2 + 1/2ρv2^2 + ρgh2
(1000000) + (.5)(1000)(10^2) + (1000)(10)(10) = P2 + (.5)(1000)(20^2) + (1000)(10)(0)
1150000= P2 + 200000 P2 = 950,000 Pa
Based on Bernoulli’s Principle, Pressure can be related to velocity. Which of the following is the proper explanation of the Bernoulli (or Venturi) Effect?
(A) As flow speed increases, pressure increases.
(B) As flow speed decreases, pressure decreases.
(C) Pressure is greater where there is more gravitational potential energy.
(D) Pressure is greater where the flow speed is lower.
(D) Pressure is greater where the flow speed is lower.
Water is flowing through a level pipe. One end of the pipe has an area of 4 m^2, while the other end has an area of 1/4 m^2. The pressure at the entrance is 200,000 Pa, while the pressure at the exit is 100,000 Pa. What is the Flow Rate in the pipe (m^3/s)?
(A) 3.54
(B) 53.33
(C) 0.8769
(D) 112.47
(A) 3.54
v1A1 = v2A2 = Flow Rate = R v1 = R/4 v2 = R/(.25) = 4R
P1 + 1/2ρv1^2 + ρgh1 = P2 + 1/2ρv2^2 + ρgh2
(200,000) + (.5)(1000)(R/4)^2 + (1000)(9.8)(h) = (100,000) + (.5)(1000)(4R)^2 +(1000)(9.8)(h)
Subtract (1000)(9.8)(h) from each side
(200,000) + (.5)(1000)(R/4)^2 = (100,000) + (.5)(1000)(4R)^2
100,000 + ( 500)(R/4)^2 = 500 (4R)^2
100,000 = 500 ((4R)^2-(R/4)^2)
simplify by actually squaring the flow rates and dividing by 500 on both sides
200=16R^2 - R^2/16
200=(255/16)R^2
12.54=R^2 (Approximately 10)
3.54=R (Approximately 3)
R = approx. 3 m^3/s (3.54 m^3/s)
As depth of fluid increases, what happens to the force of viscosity?
The force of viscosity decreases.
If the coefficient of viscosity is 4.34 Pa·s, the velocity of a boat along the surface of the liquid is 48.79 m/s, the area of the boat in contact with the fluid is 2.23 m^2, and the depth of the fluid is 5.54 m, what is the Force of viscosity on that object?
(A) 45.63
(B) 63.42
(C) 85.23
(D) 98.46
(C) 85.23
F = η A v/d F = ((4.34)(2.23)(48.79))/(5.54) F = approx. 80 N (actual: 85.23)
What happens to flow rate as the pressure gradient increases?
The flow rate increases.
A liquid is flowing through a pipe of length 4 m, with a velocity of 1000 m/s. The radius of the tube is 2 m, and there is a pressure difference of 1,000 Pa from one end of the pipe to the other. What is the coefficient of Viscosity for this fluid (in Pa*s)?
(A) 0.125
(B) 1.47
(C) 18.9
(D) 0.00232
(A) 0.125
Q = velocity x Area Q = (1000 m/s)(π(2)^2) Q = 4000π m^3/s
Q = (∆Pπr^4)/(8ηL)
4000π m^3/s = (1,000 Pa)(π)(2^4)/((8)(η)(4))
η = 16,000π/(128,000π) = 0.125 Pa·s
Blood has a Coefficient of viscosity of .004 Pa·s, and a Reynolds number of 2000. If the density of blood is 1060 kg/m^3, and the radius of the aorta is .01 m, what is the critical speed for blood in the aorta?
(A) .08
(B) .22
(C) .38
(D) .59
(C) .38
Critical speed = (Rη)/(2ρr)
Critical Speed = (2000)(.004)/((2)(1060)(.01))
Critical speed = .approx. .4 (actual: .38 m/s)
How does the critical speed change as the density of the fluid is increased?
The critical speed decreases.
What is the venturi effect?
When there is a constriction in a tube, the velocity of the fluid will increase at that point while the pressure will be lower.
This is because the same volume must flow through all parts of a connected pipe at a given time.
Which of the following correctly describes why an airplane is lifted off of the ground using the Venturi Effect?
(A) The velocity of the air under the wings is greater than the velocity of air above the wings, creating a higher pressure under the wings, giving the airplane lift.
(B) The velocity of the air under the wings is greater than the velocity of air above the wings, creating a lower pressure under the wings, giving the airplane lift.
(C) The velocity of the air under the wings is less than the velocity of air above the wings, creating a higher pressure under the wings, giving the airplane lift.
(D) The velocity of the air under the wings is less than the velocity of air above the wings, creating a lower pressure under the wings, giving the airplane lift.
(C) The velocity of the air under the wings is less than the velocity of air above the wings, creating a higher pressure under the wings, giving the airplane lift.
d
a
b
a
a
b
d
d
d
spygmomanometers
measure blood pressure
simple mercury barometer
measures incident (usually atmospheric) pressure
a mercury barometer is primarily affected by atmospheric pressure. what would happen to the level of the mercury in the column if the barometer was moved to the top of a mountain?
at the top of the mountain, atmospheric pressure is lower, causing the column to fall
a mercury barometer is primarily affected by atmospheric pressure. what would happen to the level of the mercury in the column if the barometer was placed ten meters under water?
under water, hydrostatic pressure is exerted on the barometer in addition to atmospheric pressure, causing the column to rise
ideal gas
hypothetical gas that have no intermolecular forces and no volume
ideal gas law eq
PV = nRT
n= number of moles
density eq in terms of ideal gas law
ρ = m/V = PM/RT
M = molar mass
combined gas law assumes…
number of moles stays constant
combined gas law eq
P1V1/T1 = P2V2/T2
avagadro’s principle
as the number of moles of gas increases, the volume increases in direct proportion
avogadro’s principle eq
n/V = k
n1/V1 = n2/V2
k = constant
n = number of moles
how are number of moles of gas and volume related?
directly proportional
as number of moles of gas inc, volume inc
ideal gas law
how are pressure and volume related?
inversely related
ideal gas how
how are volume and temperature related?
directly proportional
Boyle’s law eq
pressure and volume inversely related
PV = k
Can These Girls Possibly Be Virgins - draw the star of David and starting at the top (going clockwise) at every point
charles’s law eq
volume and temp are directly proportional
V/T = k
Can These Girls Possibly Be Virgins - draw the star of David and starting at the top (going clockwise) at every point
Gay Lussac’s law eq
P/T = k
Can These Girls Possibly Be Virgins - draw the star of David and starting at the top (going clockwise) at every point
ideal gas law
how are temperature and pressure related?
directly proportional
dalton’s law of partial pressures
the total. pressure of a gaseous mixture is equal to the sum of the partial pressures of the individual components
partial pressure
pressure exerted by each individual gas when in a mixture
partial pressure eq
PA = XAPT
XA = moles of Gas A / total moles of gas
PT = total pressure
vapor pressure
pressure exerted by evaporated particles above the surface of a liquid
henry’s law eq
[A] = kH x Pa
kH = henry’s constant
PA = partial pressure of A
ideal gas law
how are solubility (concentration) and pressure related?
directly related
assumptions of kinetic molecular theory
- gas volume is negligible
- gases exhibit no intermolecular forces
- gas particles are in continuous random motions
- collisions are elastic - conservation of momentum and KE
gases
how are temperature and movement of molecules related?
the higher the temp, the faster they move
gases
how are the size of molecules and their speed related?
the larger the molecules, the slower they move
kinetic molecular thoery
attempts to explain teh behavior of gas particles
graham’s law
gas diffusion
gases with lower molar masses will diffuse or effuse faster than gases with higher molar masses at the same temp
effusion
movement of gas from one compartment to another through a small opening under pressure
at what temp and pressure are deviations from ideal gas usually small?
high temp
low pressure
what happens to real gases at moderately high pressures?
occupy less volume than predicted by ideal gas law bc of intermolecular attractions
what happens to real gases at moderately low volumes or temperatures?
occupy less volume than predicted by ideal gas law bc of intermolecular attractions
what happens to real gases at extremely high pressures?
occupy more volume than predicted by ideal gas law bc particles occupy physical space
what happens to real gases at extremely low volumes or temperatures?
occupy more volume than predicted by ideal gas law bc particles occupy physical space
attractive forces between molecules will be smaller for gases that are…
small and less polarizable
attractive forces between molecules will be larger for gases that are…
polar molecules
Recall the general shape of a Phase Diagram. Under which conditions would you expect the compound to be a gas?
I would expect the gas conditions to be high temperature (right on the graph) and at lower pressures (bottom of the graph).
In a sealed balloon, there are 0.3 moles of a gas. When the temperature of the balloon increases, which of the following scenarios could NOT occur, according to the Ideal Gas Law?
(A) Increased Pressure and Volume of the balloon.
(B) Increased Pressure and Decreased Volume of the balloon.
(C) Decreased Pressure and Increased Volume of the balloon.
(D) Decreased Pressure and Volume of the balloon.
(D) Decreased Pressure and Volume of the balloon.
Because one side of the PV = nRT equation has increased (by increasing the temperature), the other side must also increase. Decreasing both Pressure and Volume could not increase the left side of the Ideal Gas Law equation, and would not occur.
If a rigid container has 1 mole of gas in it, and the pressure is increased by adding more gas from 101,325 Pa to 303,975 Pa, how much gas was added (in moles)?
(A) 1
(B) 2
(C) 3
(D) 4
(B) 2
n1 = 1 mol P1 = 101,325 Pa P2 = 303,975 Pa
Rearrange Ideal gas law: R =PV/nT
P1V1/n1T1 = P2V2/n2T2
Volume and temperature are held constant, so
P1/n1 = P2/n2
101,325/1 = 303,975/n2
n2 = 3 mol
Amount added = n2-n1 = 2 mol
Van der Waals equation can be represented as ( P0 + a(n/V)^2 )(Vc - nb) = nRT What is the difference between this and the ideal gas law (PV = nRT)? Why do we need this equation?
The Van der Waals takes into account two adjustments for the non-ideal behavior of real gases. Because the molecules of real gases take up space and have intermolecular interactions, pressure and volume need to be adjusted. This is where the a and b terms come from.
Van der Waals equation can be represented as ( P0 + a(n/V)^2 )(Vc - nb) = nRT. What do the terms a and b respectively adjust for?
a adjusts for intermolecular interactions
b adjusts for the space that molecules take up.
Explain why the modified van der Waals equation will lead to larger Pressures and smaller Volumes than are predicted by the Ideal Gas Law?
The interactions between molecules caused by Intermolecular forces will decrease the collisions, and the collisions that do occur won’t be perfectly elastic, so some energy will be lost. Attractive force between gas molecules will also contribute to the increased Pressure.
Also, the fact that the particles take up volume decreases the amount of space for particles to freely move in. Since Volume in these equations refers to unoccupied space, the Volume decreases in the van der Waals equation.
True or false? The quantities a and b in the modified van der Waals equation will be greater for larger molecules with greater intramolecular forces.
False. The quantities a and b in the modified van der Waals equation will be greater for larger molecules with greater intermolecular forces.
What is change in internal energy (ΔU) in terms of heat (Q) and work (W)?
ΔU = Q + W
ΔU = change in internal energy Q = heat put into system W = work done to system
b
a
c
a
