Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

First Aid > Behavioral Science - Epidemiology / Biostatistics > Flashcards

Behavioral Science - Epidemiology / Biostatistics Flashcards

1
Q

Cross-sectional study

  • Study Type
  • Design
  • Measures/Example
A
  • Study Type
    • Observational
  • Design
    • Collects data from a group of people to assess frequency of disease (and related risk factors) at a particular point in time.
    • Asks, “What is happening?””
  • Measures/Example
    • Disease prevalence.
    • Can show risk factor association with disease, but does not establish causality.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

Case-control study

  • Study Type
  • Design
  • Measures/Example
A
  • Study Type
    • Observational and retrospective
  • Design
    • Compares a group of people with disease to a group without disease.
    • Looks for prior exposure or risk factor.
    • Asks, “What happened?”
  • Measures/Examples
    • Odds ratio (OR).
    • “Patients with COPD had higher odds of a history of smoking than those without COPD had.”
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

Cohort study

  • Study Type
  • Design
  • Measures/Example
A
  • Study Type
    • Observational and prospective or retrospective
  • Design
    • Compares a group with a given exposure or risk factor to a group without such exposure.
    • Looks to see if exposure increased the likelihood of disease.
    • Can be prospective (asks, “Who will develop disease?”) or retrospective (asks, “Who developed the disease [exposed vs. nonexposed]?”).
  • Measures/Example
    • Relative risk (RR).
    • “Smokers had a higher risk of developing COPD than nonsmokers had.”
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

Twin concordance study

  • Design
  • Measures/Example
A
  • Design
    • Compares the frequency with which both monozygotic twins or both dizygotic twins develop same disease.
  • Measures/Example
    • Measures heritability and influence of environmental factors (“nature vs. nurture”).
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

Adoption study

  • Design
  • Measures/Example
A
  • Design
    • Compares siblings raised by biological vs. adoptive parents.
  • Measures/Example
    • Measures heritability and influence of environmental factors.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

Clinical trial

A
  • Experimental study involving humans.
  • Compares therapeutic benefits of 2 or more treatments, or of treatment and placebo.
  • Study quality improves when study is randomized, controlled, and double-blinded (i.e., neither patient nor doctor knows whether the patient is in the treatment or control group).
  • Triple-blind refers to the additional blinding of the researchers analyzing the data.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

Drug Trials: Phase I

  • Typical Study Sample
  • Purpose
A
  • Typical Study Sample
    • Small number of healthy volunteers.
  • Purpose
    • “Is it safe?”
    • Assesses safety, toxicity, and pharmacokinetics.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

Drug Trials: Phase II

  • Typical Study Sample
  • Purpose
A
  • Typical Study Sample
    • Small number of patients with disease of interest.
  • Purpose
    • “Does it work?”
    • Assesses treatment efficacy, optimal dosing, and adverse effects.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

Drug Trials: Phase III

  • Typical Study Sample
  • Purpose
A
  • Typical Study Sample
    • Large number of patients randomly assigned either to the treatment under investigation or to the best available treatment (or placebo).
  • Purpose
    • “Is it as good or better?”
    • Compares the new treatment to the current standard of care.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

Drug Trials: Phase IV

  • Typical Study Sample
  • Purpose
A
  • Typical Study Sample
    • Postmarketing surveillance trial of patients after approval.
  • Purpose
    • “Can it stay?”
    • Detects rare or long-term adverse effects.
    • Can result in a drug being withdrawn from market.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

Evaluation of diagnostic tests

A
  • Uses 2 × 2 table comparing test results with the actual presence of disease.
    • TP = true positive
    • FP = false positive
    • TN = true negative
    • FN = false negative
  • Sensitivity and specificity are fixed properties of a test (vs. PPV and NPV).
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

Sensitivity (true-positive rate)

  • Definition
  • Equations
A
  • Definition
    • Proportion of all people with disease who test positive, or the probability that a test detects disease when disease is present.
    • Value approaching 100% is desirable for ruling out disease and indicates a low false-negative rate.
    • High sensitivity test used for screening in diseases with low prevalence.
  • Equations
    • = TP / (TP + FN)
    • = 1 – false-negative rate
    • If sensitivity is 100%
      • TP / (TP + FN) = 1
      • FN = 0
      • All negatives must be TNs
  • SN-N-OUT = highly SeNsitive test, when Negative, rules OUT disease
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

Specificity (true-negative rate)

  • Definition
  • Equations
A
  • Definition
    • Proportion of all people without disease who test negative, or the probability that a test indicates non-disease when disease is absent.
    • Value approaching 100% is desirable for ruling in disease and indicates a low false-positive rate.
    • High specificity test used for confirmation after a positive screening test.
  • Equations
    • = TN / (TN + FP)
    • = 1 – false-positive rate
    • If specificity is 100%
      • TN / (TN + FP) = 1
      • FP = 0
      • All positives must be TPs
  • SP-P-IN = highly SPecific test, when Positive, rules IN disease
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

Positive predictive value (PPV)

  • Definition
  • Equation
A
  • Definition
    • Proportion of positive test results that are true positive.
    • Probability that person actually has the disease given a positive test result.
    • PPV varies directly with prevalence or pretest probability
      • High pretest probability –>Ž high PPV
  • Equation
    • = TP / (TP + FP)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

Negative predictive value (NPV) (51)

A
  • Definition
    • Proportion of negative test results that are true negative.
    • Probability that person actually is disease free given a negative test result.
    • NPV varies inversely with prevalence or pretest probability
      • High pretest probability –>Ž low NPV
  • Equation
    • = TN / (FN + TN)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

Incidence vs. prevalence

  • Equations
  • Comparison
A
  • Equations
    • Incidence rate = # of new cases in a specified time period / Population at risk during same time period
      • Incidence looks at new cases (incidents).
    • Prevalence = # of existing cases / Population at risk
      • Prevalence looks at all current cases.
  • Comparison
    • Prevalence ≈ incidence rate × average disease duration.
    • Prevalence > incidence for chronic diseases (e.g., diabetes).
    • Incidence and prevalence for common cold are very similar since disease duration is short.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

Odds ratio (OR)

  • Definition
  • Equations
A
  • Definition
    • Typically used in case-control studies.
    • Odds that the group with the disease (cases) was exposed to a risk factor (a/c) divided by the odds that the group without the disease (controls) was exposed (b/d).
  • Equations
    • OR = (a/c) / (b/d) = ad / bc
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

Relative risk (RR)

  • Definition
  • Equations
A
  • Definition
    • Typically used in cohort studies.
    • Risk of developing disease in the exposed group divided by risk in the unexposed group
    • e.g., if 21% of smokers develop lung cancer vs. 1% of nonsmokers, RR = 21/1 = 21
    • If prevalence is low, RR ≈ OR.
  • Equations
    • RR = [a / (a+b)] / [c / (c+d)]
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

Relative risk reduction (RRR)

  • Definition
  • Equations
A
  • Definition
    • The proportion of risk reduction attributable to the intervention as compared to a control.
    • e.g., if 2% of patients who receive a flu shot develop flu, while 8% of unvaccinated patients develop the flu, then RR = 2/8 = 0.25, and RRR = 1 – RR = 0.75
  • Equations
    • RRR = 1 – RR
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

Attributable risk (AR)

  • Definition
  • Equations
A
  • Definition
    • The difference in risk between exposed and unexposed groups, or the proportion of disease occurrences that are attributable to the exposure
    • e.g., if risk of lung cancer in smokers is 21% and risk in nonsmokers is 1%, then 20% (or .20) of the 21% risk of lung cancer in smokers is attributable to smoking.
  • Equations
    • AR = [a / (a+b)] - [c / (c+d)]
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

Absolute risk reduction (ARR)

  • Definition
  • Equations
A
  • Definition
    • The difference in risk (not the proportion) attributable to the intervention as compared to a control
    • e.g., if 8% of people who receive a placebo vaccine develop flu vs. 2% of people who receive a flu vaccine, then ARR = 8% - 2% = 6% = .06.
  • Equations
    • ARR = [c / (c+d)] - [a / (a+b)]
22
Q

Number needed to treat

  • Definition
  • Equation
A
  • Definition
    • Number of patients who need to be treated for 1 patient to benefit.
  • Equation
    • NNT = 1/ARR.
23
Q

Number needed to harm

  • Definition
  • Equation
A
  • Definition
    • Number of patients who need to be exposed to a risk factor for 1 patient to be harmed.
  • Equation
    • NNH = 1/AR.
24
Q

Precision

A
  • The consistency and reproducibility of a test (reliability).
  • The absence of random variation in a test.
  • Random error—reduces precision in a test.
  • Increased precision –> decreased standard deviation.
25
Q

Accuracy

A
  • The trueness of test measurements (validity).
  • The absence of systematic error or bias in a test.
  • Systematic error—reduces accuracy in a test.
26
Q

Selection bias

  • Definition
  • Examples
    • Berkson bias
    • Loss to follow-up
    • Healthy worker and volunteer biases
  • Strategies to reduce bias
A
  • Definition
    • Nonrandom assignment to participate in a study group.
    • Most commonly a sampling bias.
  • Examples
    • Berkson bias
      • A study looking only at inpatients
    • Loss to follow-up
      • Studying a disease with early mortality
    • Healthy worker and volunteer biases
      • Study populations are healthier than the general population
  • Strategies to reduce bias
    • Randomization
    • Ensure the choice of the right comparison/reference group
27
Q

Recall bias

  • Definition
  • Example
  • Strategy to reduce bias
A
  • Definition
    • Awareness of disorder alters recall by subjects
    • Common in retrospective studies.
  • Example
    • Patients with disease recall exposure after learning of similar cases
  • Strategy to reduce bias
    • Decrease time from exposure to follow-up
28
Q

Measurement bias

  • Definition
  • Example
  • Strategy to reduce bias
A
  • Definition
    • Information is gathered in a way that distorts it.
  • Example
    • Hawthorne effect — groups who know they’re being studied behave differently than they would otherwise
  • Strategy to reduce bias
    • Use of placebo control groups with blinding to reduce influence of participants and researchers on experimental procedures and interpretation of outcomes
29
Q

Procedure bias

  • Definition
  • Example
  • Strategy to reduce bias
A
  • Definition
    • Subjects in different groups are not treated the same.
  • Example
    • Patients in treatment group spend more time in highly specialized hospital units
  • Strategy to reduce bias
    • Use of placebo control groups with blinding to reduce influence of participants and researchers on experimental procedures and interpretation of outcomes
30
Q

Observer-expectancy bias

  • Definition
  • Example
  • Strategy to reduce bias
A
  • Definition
    • Researcher’s belief in the efficacy of a treatment changes the outcome of that treatment
    • aka Pygmalion effect; self-fulfilling prophecy
  • Example
    • If observer expects treatment group to show signs of recovery, then he is more likely to document positive outcomes
  • Strategy to reduce bias
    • Use of placebo control groups with blinding to reduce influence of participants and researchers on experimental procedures and interpretation of outcomes
31
Q

Confounding bias

  • Definition
  • Example
  • Strategies to reduce bias
A
  • Definition
    • When a factor is related to both the exposure and outcome, but not on the causal pathway
    • Factor distorts or confuses effect of exposure on outcome
  • Example
    • Pulmonary disease is more common in coal workers than the general population
    • However, people who work in coal mines also smoke more frequently than the general population
  • Strategies to reduce bias
    • Multiple/repeated studies
    • Crossover studies (subjects act as their own controls)
    • Matching (patients with similar characteristics in both treatment and control groups)
32
Q

Lead-time bias

  • Definition
  • Example
  • Strategy to reduce bias
A
  • Definition
    • Early detection is confused with increased survival
    • Seen with improved screening techniques.
  • Example
    • Early detection makes it seem as though survival has increased, but the natural history of the disease has not changed
  • Strategy to reduce bias
    • Measure “back-end” survival (adjust survival according to the severity of disease at the time of diagnosis)
33
Q

Measures of central tendency

  • Mean
  • Median
  • Mode
A
  • Mean = (sum of values)/(total number of values).
  • Median = middle value of a list of data sorted from least to greatest.
    • If there is an even number of values, the median will be the average of the middle two values.
  • Mode = most common value.
34
Q

Measures of dispersion

  • Standard deviation
  • Standard error of the mean
A
  • Standard deviation = how much variability exists from the mean in a set of values.
  • Standard error of the mean = an estimation of how much variability exists between the sample mean and the true population mean.
    • σ = SD, n = sample size
    • SEM = σ / sqrt(n)
    • SEM decreases as n increases
35
Q

Normal distribution

A
  • Gaussian, also called bell-shaped.
  • Mean = median = mode.
36
Q

Bimodal distribution

A
  • Suggests two different populations
  • e.g., metabolic polymorphism such as fast vs. slow acetylators; suicide rate by age
37
Q

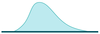
Positive skew

A
  • Typically, mean > median > mode.
  • Asymmetry with longer tail on right.
38
Q

Negative skew

A
  • Typically, mean < median < mode.
  • Asymmetry with longer tail on left.
39
Q

Null Hypothesis (H0)

A
  • Hypothesis of no difference
  • e.g., there is no association between the disease and the risk factor in the population
40
Q

Alternative Hypothesis (H1)

A
  • Hypothesis of some difference
  • e.g., there is some association between the disease and the risk factor in the population
41
Q

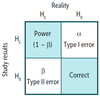
Table: Power, Type 1 Error, Type 2 Error, and Correct

42
Q

Correct result

A
  • Stating that there is an effect or difference when one exists
    • Null hypothesis rejected in favor of alternative hypothesis
  • Stating that there is not an effect or difference when none exists
    • Null hypothesis not rejected
43
Q

Type I error (α)

  • Definition
  • α & p
A
  • Definition
    • Also known as false-positive error
    • Stating that there is an effect or difference when none exists
      • Null hypothesis incorrectly rejected in favor of alternative hypothesis
    • α = you saw a difference that did not exist (e.g., convicting an innocent man).
  • α & p
    • α is the probability of making a type I error.
    • p is judged against a preset a level of significance (usually < .05).
    • If p < 0.05, then there is less than a 5% chance that the data will show something that is not really there.
44
Q

Type II error (β)

  • Definition
  • β & power
A
  • Definition
    • Also known as false-negative error.
    • Stating that there is not an effect or difference when one exists
      • Null hypothesis is not rejected when it is in fact false
    • β = you were blind to a difference that did exist (e.g., setting a guilty man free).
  • β & power
    • β is the probability of making a type II error.
    • β is related to statistical power (1 – β), which is the probability of rejecting the null hypothesis when it is false.
    • Increase power and decrease β by:
      • Increasing sample size
        • There is power in numbers.
      • Increasing expected effect size
      • Increasing precision of measurement
45
Q

Meta-analysis

A
  • Pools data and integrates results from several similar studies to reach an overall conclusion.
  • Increase statistical power.
  • Limited by quality of individual studies or bias in study selection.
46
Q

Confidence interval

  • Definition
  • Equation
  • 95% & 99% CI
  • If the 95% CI for a mean difference between 2 variables includes 0
  • If the 95% CI for odds ratio or relative risk includes 1
  • If the CIs between 2 groups do not overlap
  • If the CIs between 2 groups overlap
A
  • Definition
    • Range of values in which a specified probability of the means of repeated samples would be expected to fall.
  • Equation
    • CI = range from [mean – Z(SEM)] to [mean + Z(SEM)].
  • 95% & 99% CI
    • For the 95% CI, Z = 1.96.
      • The 95% CI (corresponding to p = .05) is often used.
    • For the 99% CI, Z = 2.58.
  • If the 95% CI for a mean difference between 2 variables includes 0
    • Then there is no significant difference and H0 is not rejected.
  • If the 95% CI for odds ratio or relative risk includes 1
    • H0 is not rejected.
  • If the CIs between 2 groups do not overlap
    • Significant difference exists.
  • If the CIs between 2 groups overlap
    • Usually no significant difference exists.
47
Q

t-test

A
  • Checks differences between means of 2 groups.
    • Tea is meant for 2
  • Example: comparing the mean blood pressure between men and women.
48
Q

ANOVA

A
  • Checks differences between means of 3 or more groups.
    • 3 words: ANalysis Of VAriance
  • Example: comparing the mean blood pressure between members of 3 different ethnic groups.
49
Q

Chi-square (χ²)

A
  • Checks difference between 2 or more percentages or proportions of categorical outcomes (not mean values).
    • Pronounce Chi-tegorical
  • Example: comparing the percentage of members of 3 different ethnic groups who have essential hypertension.
50
Q

Pearson correlation coefficient (r)

  • Definition
  • Positive vs. negative r value
  • Coefficient of determination
A
  • Definition
    • r is always between -1 and +1.
    • The closer the absolute value of r is to 1, the stronger the linear correlation between the 2 variables.
  • Positive vs. negative r value
    • Positive r value –>Ž positive correlation.
    • Negative r valueŽ –> negative correlation.
  • Coefficient of determination = r2 (value that is usually reported).
51
Q

Disease Prevention

  • Primary
  • Secondary
  • Tertiary
  • Quaternary
A
  • Primary
    • Prevent disease occurrence (e.g., HPV vaccination).
  • Secondary
    • Screening early for disease (e.g., Pap smear)
  • Tertiary
    • Treatment to reduce disability from disease (e.g., chemotherapy)
  • Quaternary
    • Identifying patients at risk of unneccessary treatment, protecting from the harm of new interventions
52
Q

Medicare and Medicaid

  • Both
  • Medicare
  • Medicaid
A
  • Both
    • Federal programs that originated from amendments to the Social Security Act.
  • Medicare
    • Available to patients ≥ 65 years old, < 65 with certain disabilities, and those with end-stage renal disease.
    • MedicarE is for Elderly
  • Medicaid
    • Joint federal and state health assistance for people with very low income.
    • MedicaiD is for Destitute

First Aid (92 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2025 Bold Learning Solutions. Terms and Conditions