ALTIUS > Physics 2 > Flashcards

Physics 2 Flashcards

(71 cards)

Study These Flashcards
1
Q
  • Think of a “FIELD” as:
A
  • an invisible influence capable of exerting a force on a MASS or CHARGE
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q
  • Universal Law of Gravitation (formula)
A

Fg=Gm1m2/r2

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q
  • The Universal Law of Gravitation is true everywhere, but NEAR EARTH’S SURFACE:
    1. What do we assume?
    2. What formula can we simplify to?
A
  • Assume g= 10 m/s2
    • Simplify to:
      • F=mg
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q
  • Give the PEgrav formula NEAR EARTH

For FLUIDS (which DON’T always move as a single uni), what change to the formula do we make?

A

PEgrav=mgh

  • For fluids:
    • use PEgrav=pgh
      • p=density=m/v

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q
  • Give the PEgravformula
    • IN SPACE, or
    • NEAR EARTH’S SURFACE
      • if we AREN’T assuming g=10 m/s2
A

PEgrav= - Gm1m2/r

Radius is NOT squared here!!!

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q
  • Friction opposes ____, not ____
A

SLIDING!

  • ​not motion

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q
  • If theres SLIDING, it’s ___ friction
  • If NOT, its ___ friction
A
  • sliding= kinetic friction
  • not sliding=static friction
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q
  • Give the formulas for static & kinetic friction
A

STATIC FRICTION:

  • Ff=UsFn ​
    • or Ff=Usmgcosθ

KINETIC FRICTION:

  • Ff=UkFn
    • or Ff=Ukmgcosθ

​Us / Uk = Coefficient of static/kinetic friction

Fs / Fk= Force of static/kinetic friction

n= “normal force”=mgcosθ

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q
  • Define MAX static friction
A
  • once this value is reached, OBJECT BEGINS TO SLIDE
    • at this moment, we now have kinetic friction, NOT STATIC

Ex: no mvmt at 500 N (static) but starts moving at 501 N=kinetic

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
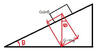
Q
  • Inclined Planes
    • Give the equation for:
      • Force down an inclined plane
        • parallel to the surface
A

F=mgsinθ

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q
  • Inclined planes:
    • Normal force on an Inclined Plane
      • Equation=?
A

Fn=mgcosθ

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q
  • Inclined planes:
    • Velocity of a particle at the base of an inclined plane
    • Equation=?
A

Vf=√2gh

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q
  • Inclined planes
    • ACCELERATION down an inclined plane
    • Equation=?
A

a=gsinθ

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

Hooke’s Law formula

A

F=kΔx

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
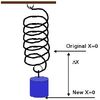
Q
  • How do you calculate k (spring constant) by hanging weights?
    • Remember calculation is different for just doing ONE trial and doing TWO (+) trials
A
  • Solve using Hooke’s Law
    • F=kΔx
    • for Δx, use:
      • _Displacement from equilibrium p_oint
        • for ONE trial
      • Difference in displacement
        • between TWO trials
    • For F, use:
      • Force applied in ONE trial, or
      • Difference in force
        • between TWO trials
  • Remember to convert mass of object to force
    • ​using F=mg
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q
  • PEelastic
    • ​Definition
    • Equation=?
A

PEelastic=½kΔx2

  • PEelastic= PE stored in a compressed spring

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q
  • PEelastic most likely used for what kinds of questions?
  • How would you use PEelastic to find out how far a spring compresses when an object hits it?
A

Conservation of energy questions!

  • When a mass of velocity V hits a spring:
    • ALL of its KE is converted into PEelastic
    • Setting KEinitial equal to final PEelastic
      • …lets you find how far the spring will compress
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q
  • Kinetic Energy equation=?
A

KE=½mv2

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q
  • Finding how far a spring compresses
    • What COMBINATION of formulas would you use?
A

Set KE equal to PEelastic

  • ​½mv2 = ½kΔx2
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
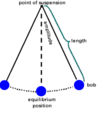
Q
  • ONE CYCLE of a pendulum is?
    • (LOTR)
A
  • “There and back again”
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q
  • For a pendulum to exhibit Simple Harmonic Motion (SHM)…
    • What value must be LOW?
A
  • Angle of displacement
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

Give 3 examples of Simple Harmonic Motion

A
  1. Pendulum
    • mass on a string
  2. Things w/ circular motion when viewed from the side
    • Ex: Something bobbing up & down in the water
      • has a circular motion!
  3. Waves sloshing back & forth in a container
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
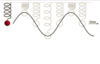
Q
  • Simple Harmonic Motion
    • Give the Mass on a Spring formula
A

T=2π√m/k

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
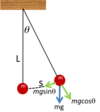
Q
  • Simple Harmonic Motion
    • Give the pendulum formula
A

T=2π√L/g

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
25
* **Simple Harmonic Motion** * What is **"T?"** * What thing is its ***inverse***?
**T=period** ## Footnote * inverse to ***frequency*** * *f=*1/T
26
* Objects **at rest** are in ___ equilibrium
***STATIC*** equilibrium
27
* Objects moving at **CONSTANT velocity** are in ___ equilibrium
***DYNAMIC*** equilibrium
28
* What do you do to solve **equilibrium** problems? * Hint: make a T...
**_Make a T_** * put **opposing** forces on **opposite** sides * **balance** them out * Ex: If 180 N in *downward* direction * then 180N *upward*
29
* Give 3 examples of **equilibrium**
1. Terminal velocity * mg=Fair 2. **Constant** velocity 3. Objects ***at rest***
30
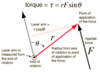
* **Torque** formulas3 variations) * Break down what each part represents
1. **T=fl** 2. **T=mgl** 3. **T=Frsinθ​** * l=lever arm * r=dist b/t force & point of rotation
31
* In Torque equation: * ***r = l*** *only* when...? * What is **always** equal to "l?"
**r = l only when θ=90°** * **"rsinθ"** is *always* equal to l
32
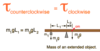
* To solve for: * **fulcrum** and **boards on strings** problems * Hint: these are in *equilibrium*
_Set:_ * **Tclockwise=Tcounterclockwise** * ​include ***ALL*** torques!
33
* Torque * In what scenario would you use ***T=Frsinθ?***
* When Force applied is ***NOT*** perpendicular to the surface * i.e., when θ is _NOT_ 90°
34
* Define: * systems ***NOT*** in equilibrium
* where the **object** has ***NON-ZERO ACCELERATION***
35
* When solving for systems NOT in equilibrium: * How do you solve it ***differently*** than systems that **are** in equilibrium? * What can you ***IGNORE*** when solving for systems that are not in equilibrium?
* Solve in **same** way as equilibrium problems (T method * but **add "ma"** to the **"losing side"** * This equals it out You can ***IGNORE SIGNS (+/-)*** when you do this method!
36
* Equilibrium on an Inclined Plane * How to solve?
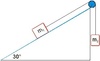
_Use T method_ * One side= ***UP*** forces * Other side=***DOWN*** forces * Down forces always equal to **F=mgsinθ** * since force of friction is always **parallel** to the plane **opposite the direction of motion**
37
How to solve problems involving ***2D*** forces
_Use T method_ * Put **formula** that **predicts component of each force** into boxes * Add "ma" onto the "losing side"
38
Define the **"right hand rule"** for **angular velocity (ω)**
* Curl fingers around axis of rotation, so that fingers are pointing in the direction of rotation * Your **thumb** will then be pointing in the **direction of the vector** (ω)
39
How many **radians** per **1 revolution**
**~6** ## Footnote * 6.28 exactly
40
How to **convert Radians** to **degrees**
* 2π radians/360° or * π radians/180°
41
* An object is in rotational equilibrium IF: * 2 options...either one or the other
1. It is ***NOT rotating***, or 2. It is rotating with **constant** ω (angular velocity)
42
* **Momentum** formula=?
**p=mv**
43
* Think of ***momentum*** as? * When is it ***always conserved***?
...as ***INERTIA INCREASED BY VELOCITY*** * p is always conserved **in an isolated system** * is not conserved when not in an isolated system
44
* Define "Impulse"
* **change** in an object's **momentum** * **"Δp"**
45
* **Impulse** formula * 3 variations (in order of *how you should think of impulse*)
1. **I=Δp** 2. **I=mΔv** 3. **I=Favgt**
46
* What are **common impulse questions**? * How are **velocity** and **impulse** related?
***CAR CRASHES!*** ## Footnote * **No** change in V= **No** impulse * **High** change in V=**High** impulse
47
* Elastic vs Inelastic collisions
_Elastic Collisions_ * p ***AND*** KE conserved _Inelastic Collisions_ * p conserved ***ONLY***
48
* If object is **deformed** during collision, it was a _____ collision
* **inelastic**
49
* Elastic collisions * Equation=? * Hint: What gets conserved during elastic collisions?
**½m1v12+ ½m2v22= ½m1v12+ ½m2v22** * p and KE both conserved
50
* For ***PERFECTLY*** elastic collisions, what 2 weird things happen? * What's a (albeit *imperfect*, but close enough) example of this?
1. ***Speed is conserved*** * before ***AND*** after collision 2. If mass of 2 objects is **equal** but they have **different velocities**: * velocities get **exchanged** * in order to **conserve momentum** (p=mv) Think of: ***BILLIARD BALLS***
51
* **Inelastic** collisions formula * What thing ***DO*** you need to remember to use here that you ***DON'T*** need to use for **elastic** collisions?
**m1v1+m2v2=m1v1+m2v2** ## Footnote You need to remember to ***USE SIGNS!! (+/-)*** * Velocity has a *negative sign* when: * going to the **LEFT** or * **DOWN**
52
* "Perfectly ***IN***elastic" collisions * definition & formula
* objects collide and **stick together** * it's like MARRIAGE! * if they move **after** collision, they do so **together** **m1v1+m2v2=(m1+m2)v3**
53
* **Reverse Collisions** definition * What is commonly use by the MCAT to test you on **reverse** collisions?
* Two objects **start out together** and **come apart** * it's like DIVORCE _Common examples:_ * Bomb exploding * Also, RADIOACTIVE DECAY is frequently used
54
* **Thermal expansion** formula
ΔL=αLoΔT
55
* Heating solids leads to \_\_\_ * Cooling solids leads to \_\_\_
* expansion * shrinkage
56
* What makes water ***unique*** when it comes to **thermal expansion?**
* When temperature of water gets close to zero, it ***EXPANDS (INSTEAD OF SHRINKING)*** * because of of *highly ordered lattice structure* of ice * This is why the solid ice doesnt sink on liquid water
57
* PEelec * formula=? * 2 variations
* **PEelec=Kq1q2/r** or * **PEelec=qEd**
58
* PEcapacitor formula=? * 3 variations
* **PEcapac=½QV** * **PEcapacitor=½CV2** * **PEcapacitor=½Q2/C**
59
* **Internal** energy * definition
* Energy of: * **Internal vibrations** & * **Random motions** of: * molecules and/or * atoms w/ ...in a system
60
* Heat energy * Definition * Where can Heat Energy **come from?** (2)
**=energy dissapated as heat** ## Footnote * _Can come from:_ 1. a collision 2. a current-carrying wire (among other things)
61
* **Law** of **Conservation of Energy** says...?
* in an **isolated** system: * energy is _***ALWAYS*** ***CONSERVED***_ * e.g., it can be **transferred**, but **never lost**
62
* Define an **"Open system"**
* both **mass *AND* energy** * **​...**can be **exchanged** with surroundings
63
Define a **"Closed system"**
* **Energy**, but ***NOT mass*** * ...can be exchanged with the surroundings
64
* Define an **"Isolated system"**
* ***Neither mass NOR energy*** * ***​...***can be exchanged with the surroundings
65
* Think of "Work" in what order? * ...when it comes to ***formulas***
1. **W=ΔE** 2. **W=Fdcosθ**
66
* When I see the following, Ill think "WORK" * 7 things
1. Change in **velocity** 2. Change in **height** 3. Change in **positon of masses** (or planets in space) 4. Change in **position of a charge** 5. **Compression** of a spring (PE stored up) 6. Friction 7. Air resistance
67
* Give 2 examples of **W=Fdcosθ​** * aka...give 2 examples of **force** being applied **along a displacement**
1. Pushing a block along a table 2. An object falling from height * height=displacement! * Dont forget that!
68
* What are the **ONLY** 2 ways energy can be transferred in/out of a system?
1. Work 2. Heat (dissapated)
69
* 1st Law of Thermodynamics * Equation=?
**ΔE= W + Q**
70
* Work-Energy theorem * What should you focus on **instead**?
* If Fnet does work on a **rigid** object: * the **work done** on that object is equal to: * the **change in KE** of the object * Focus on W=ΔE * correct use of this **negates** need to use work-energy theorem
71
ALTIUS
flashcards
Decks in class (27)
# Cards
Brainscape helps you reach your goals faster, through stronger study habits.
© 2026 Bold Learning Solutions. Terms and Conditions